| 컬럼니스트 : | 연주영 원장 |
|---|---|
| 컬럼지 : | 한국일보 |
| 날짜 : | 2014-09-02 |
우리는 자연적 현상(Natural Phenomena)을 경험하고 산다. 매일 해는 떠오르고, 산천은 철따라 고운 옷을 갈아입으며, 가을은 우리를 반겨준다. 어떤 사건이 정규적으로 일어날 때에는 통계를 낼수 있다. 그리고, 확률은 그래프로 쉽게 설명될 수 있다.
프랑스의 통계학자(statistician) 아브라함 드 무아브르 (Abraham de Moivre 1667~1754)는 동전을 100번 이상 던져서 그래프를 그렸을 때에, 중간 부분이 점점 곡선으로 나타내는 정규 곡선(Normal Curve)을 발견하였다.
그의 바톤을 이어받아 연구하여 공식(formula)으로 완성시킨 수학자는 가우스 (Johann C.F. Gauss, 1777-1855)이다. 그는 보통30번 이상 반복되는 일들을 정규 분포(Normal Distribution) 그래프로 표현했을 때에, 설령 어느 정도의 오차(error)가 생기더라도 정규 분포 곡선이 나타난다는 것을 확인하였다. 그래프의 모든 윗 부분을 매끄럽게 연결하면 종(bell)모양의 실루엣(silhouette)이 그려지기에, 쉽게 벨 커브(Bell Curve)라는 새로운 용어를 탄생시켜(coin) 부르게 되었다.
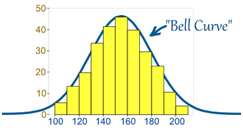
그리고, 이 그래프는 미국 사회를 상징하는 대표적인 상징이 되었다. 미국 사람들은 사회가 건강할수록 중상층(Middle Class)이 주축이 되어야 한다고 생각한다. 그래서, 이 사회는 벨 커브, 즉 중상층의 곡선의 그림을 유지 하려고 노력 하고 있다.
교육계에서도 이 정규 분포 곡선(Normal Distribution Curve)은 고급 학습 과정에서 큰 의미를 가지고 있다. 예를 들어, 10월에 치뤄지는 PSAT로 시작해서 대학원 시험까지 벨 커브가 그려지면 훌륭한 시험이라고 간주하며 벨 커브가 한쪽으로 치우쳤을 때에는 시험은 새로 디자인 되어야 된다고 생각한다.
벨 커브의 양쪽 끝을 가면 갈수록 확률이 급격히 작아진다. 우열(superiority)을 확실하게 가려낼 수 있게 보여주며, 양분 된다. 이 벨 커브에 최상, 평균, 최하가 명백하게 그려지는 것이다.
벨 커브는 우리 실생활에서도 늘 사용되고 있다. 연령에 맞는 표준 몸무게와 키를 알수 있는 것도 벨 커브 덕분이다. 이제, 학업에 대한 벨 커브를 생각해 보아야 할 시기가 되었다. 벨 커브를 이해 한다면, 그 만큼 성공 확률이 높아 지기 때문이다.















 이곳 교육 컬럼은
현재 Seed 학원 원장이신 연주영 원장께서 한국일보에 기고하신 교육 컬럼 입니다.
이곳 교육 컬럼은
현재 Seed 학원 원장이신 연주영 원장께서 한국일보에 기고하신 교육 컬럼 입니다.